

In this section, we explore integrals containing expressions of the form \(\sqrt\), \(\sqrt\), and \(\sqrt\), where the values of \(a\) are positive. We have already encountered and evaluated integrals containing some expressions of this type, but many still remain inaccessible. The technique of trigonometric substitution comes in very handy when evaluating these integrals. This technique, which is a specific use of the Substitution Method, rewrites these integrals as trigonometric integrals.
Before diving into the instruction, it's best to recall the following identities from Trigonometry (all based on the Pythagorean Identity):
Note that the forms of these expressions match the radicands in
This observation will be very powerful and you should spend some time convincing yourself that these forms are, indeed, incredibly similar.
The final bit of "recall" we will need prior to developing the method of trigonometric substitution are the ranges of the inverse trigonometric functions. Specifically, we will need to remember, from Section 1.6 in the Differential Calculus textbook, the following range restrictions:
\[ \begin
\sin^(y) = \theta & \text < if and only if >& \sin(\theta) = y & \text < where >& \theta \in \left[−\frac< \pi >, \frac< \pi > \right] \\
\tan^(y) = \theta & \text < if and only if >& \tan(\theta) = y & \text < where >& \theta \in \left(−\frac< \pi >, \frac< \pi > \right) \\
\sec^(y) = \theta & \text < if and only if >& \sec(\theta) = y & \text < where >& \theta \in \left[0, \frac<\pi> \right) \cup \left[ \pi, \frac \right). \\
\end \nonumber \]
You should already be comfortable with the restrictions on \( \theta \) for both the arcsine and arctangent from your Trigonometry or Precalculus course; however, the following snippet from Section 1.6 in the Differential Calculus textbook should begin to justify our choice of range for the arcsecant.
All the inverse trigonometric functions return angles in quadrant I (where all trigonometric functions are positive) and one other quadrant where the corresponding trigonometric function is negative. The returned quadrants where the corresponding trigonometric functions are negative are fairly standard and agreed upon (quadrant IV for arctangent and arcsine, and quadrant II for arccosine and arccotangent); however, the quadrants chosen for the ranges of the arcsecant and arccosecant are not universally agreed upon.
In this text, we choose arcsecant and arccosecant to return angles in quadrants I and III for a special reason - it makes our work in calculus slightly easier. I mention this because you might have seen a slightly different choice for the ranges of these functions in another textbook. The difference is insignificant other than the ease our choice makes for our work in calculus.
Before developing a general strategy for integrals containing \(\sqrt\), consider the integral \(\displaystyle \int \sqrt \, dx.\) This integral cannot be evaluated using any of the techniques we have discussed so far. However, if we make the substitution \(x=3\sin \theta \), we have \(dx=3\cos \theta \, d \theta .\) After substituting into the integral, we have
\[ \int \sqrt\,dx= \int \sqrt< 9−(3\sin \theta )^2>\cdot 3\cos \theta \,d \theta . \nonumber \]
After simplifying, we have
\[ \int \sqrt< 9−x^2>\,dx= \int 9 \sqrt\cdot\cos \theta \, d \theta . \nonumber \]
Letting \(1−\sin^2 \theta =\cos^2 \theta ,\) we now have
\[ \int \sqrt< 9−x^2>\,dx= \int 9 \sqrt\cos \theta \, d \theta . \nonumber \]
Assuming that \(\cos \theta \geq 0\), 1 we have
\[ \int \sqrt< 9−x^2>\,dx= \int 9\cos^2 \theta \, d \theta . \nonumber \]
At this point, we can evaluate the integral using the techniques developed for integrating powers and products of trigonometric functions. Before completing this example, let’s take a look at the general theory behind this idea.
To evaluate integrals involving \(\sqrt\), we make the substitution \(x=a\sin \theta \) and \(dx=a\cos \theta \, d \theta \). To see that this actually makes sense, consider the following argument: The domain of \(\sqrt\) is \([−a,a]\). Thus,
Since \(\cos \theta \geq 0\) on \(−\frac< \pi > \leq \theta \leq \frac< \pi >\) and \(a \gt 0\), \(|a\cos \theta |=a\cos \theta\).
Therefore, by making the substitution \(x=a \sin \theta \), we are able to convert an integral involving a radical into an integral involving trigonometric functions, where we have the added benefit on not having to worry about absolute values. From this point, we need to evaluate the integral. Once this is done, however, we are required to convert the solution back to an expression involving \(x\). To do this, we begin by drawing a reference triangle for \( \theta \) (see Figure \( \PageIndex \)).

Since \( -\frac<\pi> \leq \theta \leq \frac<\pi> \), this reference triangle can only be drawn in quadrants I or IV. In either case,
Hence, no matter what trigonometric function is in the result of our evaluated integral, we can rewrite it as a function of \( x \). Should \( \theta \) appear by itself, we use \( \theta =\sin^\left(\frac\right)\). 2
The essential part of this discussion is summarized in the following problem-solving strategy.
The following example demonstrates the application of this problem-solving strategy.
Note that a simple (non-trigonometric) \( u \)-substitution will not work here. Therefore, begin by making the substitutions \(x=3\sin \theta \) and \(dx=3\cos \theta \, d \theta\). Since \(\sin \theta =\frac\), we can construct the reference triangle shown in Figure \( \PageIndex \).
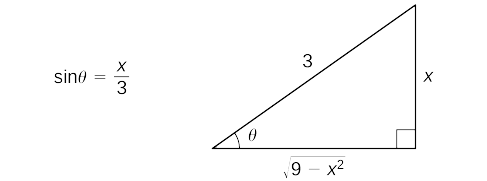
\[ \begin
\displaystyle \int \sqrt\,dx & = & \displaystyle \int \sqrt < 9−(3\sin \theta )^2>\cdot 3\cos \theta \,d \theta & \left( \textx=3\sin \theta\text< and >dx=3\cos \theta \,d \theta. \right) \\
& = & \displaystyle \int \sqrt< 9(1−\sin^2 \theta )>\cdot 3\cos \theta \, d \theta & \\
& = & \displaystyle \int \sqrt< 9\cos^2 \theta >\cdot 3\cos \theta \, d \theta & \left( \text\cos^2 \theta =1−\sin^2 \theta. \right) \\
& = & \displaystyle \int 3|\cos \theta |3\cos \theta \, d \theta & \left( \text \right) \\
& = & \displaystyle \int 9\cos^2 \theta \, d \theta & \left( \text−\dfrac< \pi > \leq \theta \leq \dfrac< \pi >\text\cos \theta \geq 0\text< and >|\cos \theta |=\cos \theta . \right) \\
& = & \displaystyle \int 9\left(\dfrac+\dfrac\cos(2 \theta )\right)\,d \theta & \\
& = & \dfrac \theta +\dfrac\sin(2 \theta )+C & \\
& = & \dfrac \theta +\dfrac(2\sin \theta \cos \theta )+C & \left( \text \right) \\
& = & \dfrac\sin^\left(\dfrac\right)+\dfrac \cdot \dfrac \cdot \dfrac<\sqrt>+C & \left( \text\sin^\left(\dfrac\right)= \theta\text < and use the reference triangle.>\right) \\
& = & \dfrac\sin^\left(\dfrac\right)+\dfrac
\end \nonumber \]
Example \( \PageIndex \) showcases something that I tell my students repeatedly - Mastery of Trigonometry is a requirement for your success in Calculus. If you need to brush up on lost Trigonometry skills, please see Section 1.6 of the Differential Calculus textbook for a single-section review of all basic material required from Trigonometry for survival in Calculus. There are more topics required from your Trigonometry and/or Precalculus course than what is shown in that section; however, those missing topics (e.g., polar coordinates and parametric equations) are reviewed later.
While it might look like a simple, non-trigonometric \( u \)-substitution is viable here, it's not.
We want \( \frac x^2 = 4 \sin^2 \theta \), so we make the substitution \( \frac x = 2 \sin \theta \), which leads to \( \frac \, dx = 2 \cos \theta \, d \theta \). Solving this for \( dx \), we get \( dx = \frac \cos \theta \, d \theta \). We will also need to know what \( x \) is in terms of \( \theta \) for that denominator. Collecting everything in a nice group, we have the following:
As in Example \( \PageIndex \), we draw a reference triangle to help our conversions and we get
\[ \begin
\displaystyle \int \dfrac x^2>>\,dx & = & \displaystyle \int \dfrac>> \sin \theta > \cdot \cancel> \cos \theta \, d \theta & \\
& = & \displaystyle \int \dfrac\,d \theta & \\
& = & \displaystyle \int \dfrac<2(1−\sin^2 \theta )>\,d \theta & \\
& = & \displaystyle \int (2\csc \theta −2\sin \theta )\,d \theta & \\
& = & 2 \ln |\csc \theta −\cot \theta |+2\cos \theta +C & \\
& = & 2 \ln \left|\dfrac−\dfrac x^2>>\right|+\sqrt x^2>+C & \left( \text \right) \\
& = & 2 \ln \left|\dfrac>\right|+\dfrac \sqrt+C & \\
\end \nonumber \]
In the next example, we see that we sometimes have a choice of methods.
Evaluate \( \displaystyle \int x^3\sqrtdx\) two ways: first by using the substitution \(u=1−x^2\) and then by using a trigonometric substitution.
Let \(u=1−x^2\). Hence, \(x^2=1−u\). Thus, \(du=−2x\,dx\). In this case, the integral becomes
Let \(x=\sin \theta \). In this case, \(dx=\cos \theta \, d \theta\). Using this substitution, we have
\[ \begin
\displaystyle \int x^3\sqrt\,dx & = & \displaystyle \int \sin^3 \theta \cos^2 \theta \, d \theta & \\
& = & \displaystyle \int (1−\cos^2 \theta )\cos^2 \theta \sin \theta \, d \theta & \\
& = & \displaystyle \int (u^4−u^2)\,du & \left( \textu=\cos \theta\text<. Thus, >du=−\sin \theta \, d \theta .\right) \\
& = & \dfracu^5−\dfracu^3+C & \\
& = & \dfrac\cos^5 \theta −\dfrac\cos^3 \theta +C & \\
& = & \dfrac(1−x^2)^−\dfrac(1−x^2)^+C & \left( \text \right) \\
\end \nonumber \]
Rewrite the integral \(\displaystyle \int \dfrac>\,dx\) using the appropriate trigonometric substitution (do not evaluate the integral).
Hint
Substitute \(x=5\sin \theta \) and \(dx=5\cos \theta \, d \theta .\)
Answer
\(\displaystyle \int 125\sin^3 \theta \, d \theta \)
1 We will justify this assumption momentarily.
For integrals containing \(\sqrt\), let’s first consider the domain of this expression. Since \(\sqrt\) is defined for all real values of \(x\), we restrict our choice to those trigonometric functions that have a range of all real numbers. Thus, our choice is restricted to selecting either \(x=a\tan \theta \) or \(x=a\cot \theta \). Either of these substitutions would actually work, but the standard substitution is \(x=a\tan \theta \) or, equivalently, \(\tan \theta = \frac\). With this substitution, we make the assumption that \(−\frac<\pi> \lt \theta \lt \frac<\pi>\), so that we also have \( \theta =\tan^\left( \frac \right)\). As before, let's derive the concept.
Since \(\sec \theta \geq 0\) on \(−\frac< \pi > \lt \theta \lt \frac< \pi >\) and \(a \gt 0\), \(|a\sec \theta |=a\sec \theta\).
We again arrive at the beautiful result that making the substitution \(x=a \tan \theta \) allows us to convert an integral involving a radical into an integral involving trigonometric functions, where we have the added benefit on not having to worry about absolute values. To convert our solution back to an expression involving \(x\), we draw a reference triangle for \( \theta \) (see Figure \( \PageIndex \)).
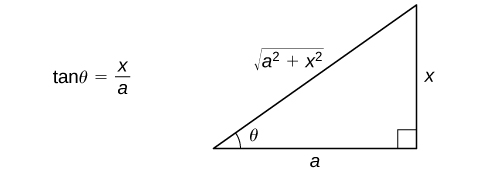
Since \( -\frac<\pi> \lt \theta \lt \frac<\pi> \), this reference triangle can only be drawn in quadrants I or IV. In either case,
Hence, no matter what trigonometric function is in the result of our evaluated integral, we can rewrite it as a function of \( x \). Should \( \theta \) appear by itself, we use \( \theta =\tan^\left(\frac\right)\). The procedure for using this substitution is outlined in the following problem-solving strategy.
Evaluate \(\displaystyle \int \dfrac>\) and check the solution by differentiating.
Begin with the substitution \(x=\tan \theta \) and \(dx=sec^2 \theta \,d \theta \). Since \(\tan \theta =x\), draw the reference triangle in Figure \(\PageIndex\).
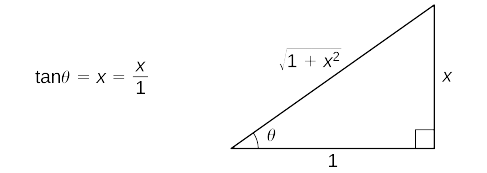
\[\begin
\displaystyle \int \dfrac> & = & \displaystyle \int \dfrac \, d \theta & \bigg(\textx=\tan \theta \text< and >dx=\sec^2 \theta \, d \theta . \\
& & & \text\sqrt=\sec \theta .\bigg) \\
& = & \displaystyle \int \sec \theta \, d \theta & \\
& = & \ln |\sec \theta +\tan \theta |+C & \\
& = & \ln |\sqrt+x|+C & \left(\text \right) \\
\end \nonumber \]
To check the solution, differentiate:
Since \(\sqrt+x \gt 0\) for all values of \(x\), we could rewrite \( \ln |\sqrt+x|+C= \ln (\sqrt+x)+C\), if desired.
In Differential Calculus, you learned about the hyperbolic functions, their inverses, and the derivatives of both the base hyperbolic functions and their inverses. At the time, it was very likely that you were not required to memorize the derivatives of the inverse hyperbolic functions; however, if you happened to have stored those derivatives in your brain, then Example \( \PageIndex \) could be much easier. Let's take a look at what I mean.
Use the substitution \(x = \sinh t \) to evaluate \(\displaystyle \int \dfrac>.\)
Because \(\sinh t \) has a range of all real numbers, and \(1+\sinh^2 t =\cosh^2 t \), we may use the substitution \(x=\sinh t \) to evaluate this integral. In this case, \(dx=\cosh t \,dt\), Consequently,
\[\begin
\displaystyle \int \dfrac> & = & \displaystyle \int \dfrac> \, dt & \left( \textx=\sinh t \text< and >dx=\cosh t \, dt .\right) \\
& = & \displaystyle \int \dfrac> \, dt & \left(\text1+\sinh^2 t =\cosh^2 t . \right) \\
& = & \displaystyle \int \dfrac <|\cosh t |>\, dt & \\
& = & \displaystyle \int \dfrac \, dt & \left(|\cosh t |=\cosh t \text< since >\cosh t \gt 0 \text < for all >t .\right) \\
& = & \displaystyle \int \, dt & \\
& = & t + C & \\
& = & \sinh^ x + C & \\
\end \nonumber \]
Example \( \PageIndex \) deserves a couple comments. First, I did not use \( \theta \) as the argument for \( \sinh \) and \( \cosh \) because we traditionally reserve \( \theta \) for angles. The argument of the hyperbolic functions are not angles, so it's a bit safer to use a variable that does not invoke thoughts of angles. If you were not aware of this fact, please see Section 1.7 of the Differential Calculus textbook for a discussion of the fact that the arguments of the hyperbolic functions are neither angles nor arc lengths.
The second comment is a continuation of my comments prior to Example \( \PageIndex \). Had we recalled that
we would have easily finished Example \( \PageIndex \) in a single step; however, the answers to Examples \( \PageIndex \) and \( \PageIndex \) don't appear to match. In order to rectify this, we would need to recall that
Find the length of the curve \(y=x^2\) over the interval \(\left[0,\frac\right]\).
Because \(\frac=2x\), the arc length is given by
To evaluate this integral, use the substitution \(x = \frac\tan \theta \) and \(dx = \frac \sec^2 \theta \, d \theta \). We also need to change the limits of integration. If \(x = 0\), then \( \theta = 0\) and if \(x=\frac\), then \( \theta =\frac< \pi >.\) Thus,
\[ \begin
\displaystyle \int^_0 \sqrt \, dx & = & \displaystyle \int^<\pi/4>_0 \sqrt \cdot \dfrac \sec^2 \theta \, d \theta \\
& = & \dfrac \displaystyle \int ^< \pi /4>_0 \sec^3 \theta \, d \theta \\
& = & \dfrac \left( \dfrac\sec \theta \tan \theta + \dfrac\ln |\sec \theta +\tan \theta | \right) \bigg|^<\pi/4>_0 \\
& = & \dfrac\left( \sqrt + \ln(\sqrt+1) \right). \\
\end \nonumber \]
Rewrite \(\displaystyle \int x^3\sqrtdx\) by using a substitution involving \(\tan \theta \).
Hint
Use \(x=2\tan \theta \) and \(dx=2\sec^2 \theta \, d \theta .\)
Answer
\[ \int 32\tan^3 \theta \sec^3 \theta \, d \theta \nonumber \]
3 The idea of constantly checking to see if something from the past will work first (i.e., a simple \( u \)-substitution) should not be new to you - especially if you took Differential Calculus using this text (well, the Calculus I version, at least). In that text, I continually referenced the Mathematical Mantra. The Mathematical Mantra boils down to doing mathematics in the order you learned mathematics - Arithmetic before Algebra, Algebra before Trigonometry, Trigonometry before Precalculus, Precalculus before Differential Calculus, and, in this case, Differential Calculus before Integral Calculus. In Differential Calculus, you learned about the Substitution Method. If you can evaluate an integral using the Substitution Method, then there is no need to get any fancier than that - don't jump to Trigonometric Substitutions, Integration by Parts, or any other, more obscure, technique if a good 'ol \( u \)-substitution does the job.
4 As was stated previously, if given a definite integral, then you are expected to be able to evaluate the arctangent at special ratios.
5 The reference triangle is based on the assumption that \(x \gt 0\); however, the trigonometric ratios produced from the reference triangle are the same as the ratios for which \(x \leq 0\).
Since the range of \(\sec \theta\) over \(\left[0, \frac<\pi>\right) \cup \left[ \pi, \frac \right) \) is \((-\infty, -1] \cup [1, \infty)\), there is a unique angle \( \theta \) satisfying \(0 \leq \theta \lt \frac<\pi>\) or \( \pi \leq \theta \lt \frac \) so that \(\sec \theta = \frac\), or equivalently, so that \(x=a\sec \theta \). If we substitute \(x=a\sec \theta \) into \(\sqrt\), we get
Since \(\tan \theta \geq 0\) on \(0 \leq \theta \lt \frac< \pi >\) and \( \pi \leq \theta \lt \frac \), and because \(a \gt 0\), \(|a\tan \theta |=a\tan \theta\).
Once more, by making the substitution \(x=a \sec \theta \), we can convert an integral involving a radical into an integral involving trigonometric functions, where we have the added benefit on not having to worry about absolute values. To convert our solution back to an expression involving \(x\), we draw a reference triangle for \( \theta \) (see Figure \( \PageIndex \) below).

Since \( \theta \in \left[ 0, \frac<\pi> \right) \cup \left[\pi, \frac \right) \), this reference triangle can only be drawn in quadrants I or III. 7 In either case,
Hence, no matter what trigonometric function is in the result of our evaluated integral, we can rewrite it as a function of \( x \). Should \( \theta \) appear by itself, we use \( \theta =\sec^\left(\frac\right)\). The procedure for using this substitution is outlined in the following problem-solving strategy.
The procedure for using this substitution is outlined in the following problem-solving strategy.
Find the area of the region between the graph of \(f(x)=\sqrt\) and the x-axis over the interval \([3,5].\)
First, sketch a rough graph of the region described in the problem, as shown in the following figure.
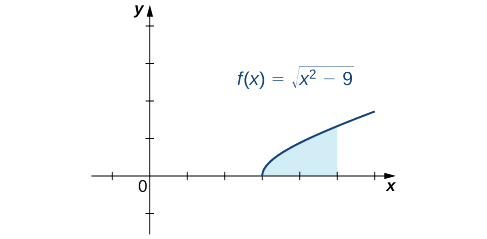
We can see that the area is \(A= \int ^5_3\sqrt \, dx\). To evaluate this definite integral, substitute \(x=3\sec \theta \) and \(dx=3\sec \theta \tan \theta \, d \theta \). We must also change the limits of integration. If \(x=3\), then \(3=3\sec \theta \) and hence \( \theta =0\). If \(x=5\), then \( \theta =\sec^(\frac)\). After making these substitutions and simplifying, we have
\[ \begin
\text & = & \displaystyle \int ^5_3 \sqrt \, dx & \\
& = & \displaystyle \int ^(5/3)>_0 9\tan^2 \theta \sec \theta \, d \theta & \\
& = & \displaystyle \int ^(5/3)>_0 9(\sec^2 \theta −1)\sec \theta \, d \theta & \left( \text\tan^2 \theta =\sec^2 \theta - 1. \right) \\
& = & \displaystyle \int ^(5/3)>_0 9(\sec^3 \theta −\sec \theta )\,d \theta & \\
& = & \left( \dfrac \ln |\sec \theta +\tan \theta | + \dfrac \sec \theta \tan \theta − 9 \ln |\sec \theta +\tan \theta | \right) \bigg|^(5/3)>_0 & \\
& = & \left( \dfrac \sec \theta \tan \theta − \dfrac \ln |\sec \theta +\tan \theta | \right) \bigg|^(5/3)>_0 & \\
& = & \dfrac \cdot \dfrac \cdot \dfrac − \dfrac \ln \left| \dfrac+\dfrac \right| − \left( \dfrac \cdot 1 \cdot 0 − \dfrac \ln |1+0| \right) & \\
& = & 10 - \dfrac \ln 3 & \\
\end \nonumber \]
Evaluate \[ \int \dfrac>. \nonumber \]Assume that \(x \gt 2.\)
Hint
Substitute \(x=2\sec \theta \) and \(dx=2\sec \theta \tan \theta \, d \theta .\)
Answer
6 Of the three processes we have developed, it is important to pay close attention to this one in particular. The reason behind choice of restriction for the range from Section 1.6 in the Differential Calculus textbook of the arcsecant should become apparent.
7 Again, this is the distinct difference between the previous two derivations and this one. It is very important to note that we could have used the non-elegant range restriction of \( \theta \in \left[0 , \frac<\pi> \right) \cup \left( \frac<\pi>, \pi \right] \) for the arcsecant; however, doing so would result in a more complex derivation of this trigonometric substitution due to the sign of the tangent in quadrant II being negative - this would not allow for \( |a \tan \theta | = a \tan \theta \).
There are many situations in which a given integral seems too challenging to be evaluated using known techniques. In these (and, in fact, in all) cases, you should remember the Mathematical Mantra:
Perform mathematics in the order you learned mathematics. That is, perform
Arithmetic before Algebra,
Algebra before Trigonometry,
Trigonometry before Precalculus, and
Precalculus before Differential Calculus.
Always be willing to ask yourself, "Is there something I learned previously that can simplify my work here?"
The following example illustrates how using the Mathematical Mantra can reduce a seemingly impossible problem into a more manageable one.
Evaluate the integral.
Think of all the methods we have so far to help us evaluate integrals:
. however, now that we have exhausted all our integration techniques learned up to this point, we should realize that there must be some type of manipulation of the integrand using our previously learned mathematics to help us out.
There are, in fact, two previously learned topics in mathematics that can help here - both from algebra; however, I will only mention completing the square as the other topic will lead to an integral we do not yet have a way to evaluate.
Back in Algebra (Algebra I, in fact), we learned how to complete the square for quadratic functions. This idea is incredibly helpful with the given integral.
\[ 3 + 4x - 4x^2 = -4(x^2 - x) + 3 = -4\left( x^2 - x + \left( -\frac \right)^2 \right) + 3 + 4 \left( - \frac \right)^2 = -4 \left( x - \frac \right)^2 + 4 = 4 - 4 \left( x - \frac \right)^2. \nonumber \]
The denominator of the integrand includes a difference of squares. This should encourage us to try a trigonometric substitution. The form is \( a^2 - x^2 \), which reminds us of the trigonometric identity \( 1 - \sin^2 \theta = \cos^2 \theta \). Hence, we want \( \left( x - \frac \right)^2 = a^2 \sin^2 \theta = \sin^2 \theta \), which gives \( x - \frac = \sin \theta \). Moreover, this gives \( dx = \cos \theta \, d \theta \). Finally, the numerator of the integrand has \( x^2 \), so it is necessary to determine \( x \) as a function of \( \theta \). Since \( x - \frac = \sin \theta \), \( x = \sin \theta + \frac \), and so \( x^2 = \left(\sin \theta + \frac\right)^2 \). Summarizing, we have
Moreover, it's a good idea to draw a reference triangle at this point. Figure \( \PageIndex \) shows our reference triangle.
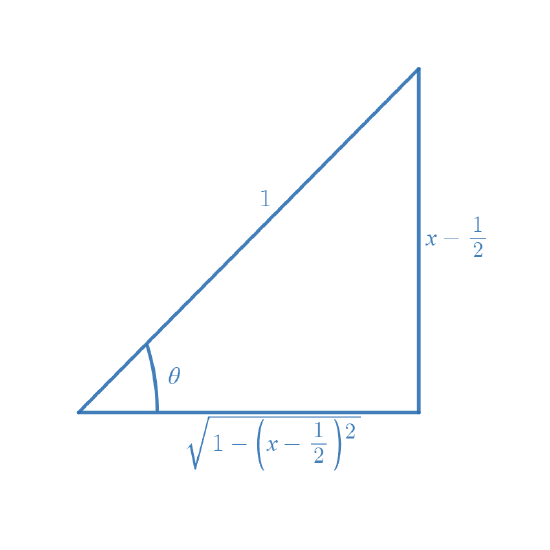
Figure \( \PageIndex \): The reference triangle.
8 We have learned enough integration techniques at this point to realize that the Substitution Method is an "umbrella method" encapsulating at least two different "types" of substitution. The first was simple \( u \)-substitution from our Differential Calculus course. The second, which we were introduced to in this section, is trigonometric substitutions.
trigonometric substitution an integration technique that converts an algebraic integral containing expressions of the form \(\sqrt\), \(\sqrt\), or \(\sqrt\) into a trigonometric integral
This page titled 2.3: Trigonometric Substitution is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Roy Simpson.